Kebalikan teorema Pythagoras pada dasarnya merupakan sutu cara untuk
menentukan jenis segitiga jika panjang sisi-sisinya diketahui. Dengan kata
lain, kebalikan teorema Pythagoras digunakan untuk melihat apakah segitiga itu
siku-siku, lancip, atau tumpul. Untuk menentukan jenis-jenis segitiga
berdasarkan panjang sisi-sisinya, maka kita harus menentukan sisi terpanjangnya
terlebih dahulu. Sisi terpanjang inilah yang kemudian kita jadikan patokan
untuk menentukan jenis segitiga.
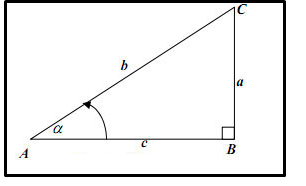
Pada segitiga ABC jika panjang a, b, dan c diketahui,
maka untuk menyelidiki jenis segitiganya kita dapat menggunakan prinsip
kebalikan teorema Pythagoras, yaitu:
- Jika a²
= b² + c², segitiga ABC siku-siku
- Jika a² < b² + c²,
segitiga ABC siku-siku
- Jika a² > b² + c²,
segitiga ABC siku-siku
Untuk segitiga siku-siku, kita bisa menentukan letak siku-sikunya
berdasarkan tiga kemungkinan berikut:
- Jika a²
= b² + c², segitiga ABC siku-siku di A
- Jika b² = a² + c², segitiga ABC siku-siku
di B
- Jika c² = a² + b², segitiga ABC siku-siku
di C
Contoh
Soal 1
Diketahui ΔABC dengan AB = 4 cm, AC = 3 cm dan BC
= 6 cm. Tentukan jenis segitiga ABC, apakah segitiga lancip,
siku-siku, atau tumpul.
Jawab:
BC adalah sisi
terpanjang ΔABC.
BC² ↔ AC² + AB²
6² ↔ 3² + 4²
36 ↔ 9+16
36 > 25
Maka segitiga
tersebut adalah segitiga tumpul.
Contoh
Soal 2
Diketahui ΔKLM dengan KL = 13 cm, LM = 12 cm dan KM
= 5 cm. Tentukan jenis segitiga KLM, apakah segitiga lancip,
siku-siku, atau tumpul.
Jawab:
KL adalah sisi
terpanjang ΔKLM.
KL² ↔ LM² + KM²
13² ↔ 12² + 5²
169 ↔ 144 + 25
169 = 169
Maka segitiga
tersebut adalah segitiga siku-siku.
REFERENSI
https://sites.google.com/view/fhlv-edu/materi/teorema-pythagoras/kebalikan-teorema-pythagoras





0 Komentar